유클리드 호제법이란?
호제법이란 말은 두 수가 서로 상대방 수를 나누어서 결국 원하는 수를 얻는 알고리즘을 나타낸다.
호제법(互除法)이라는 단어가 따로 있는것은 아니고, 서로(互) 나누기(除) 때문에 붙여진 이름이다.
유클리드 호제법의 정의는 다음과 같다.
자연수 a, b에 대해서 a를 b로 나눈나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다.
즉, gcd(a, b)=gcd(b,r) 이라고 나타낼 수 있다.
영어로 유클리드 호제법은 Euclidean algorithm 이다. 말 그대로 알고리즘이기 때문에, 유클리드 호제법을 한번만 사용해서는 큰 의미가 없고,, b를 r로 나눈 나머지 r'를 구하고, 다시 r을 r'로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 될때까지 연속해서 사용한다. 나머지가 0이 될때, 나누는 수가 a와 b의 최대공약수임을 구해낼 수 있다.
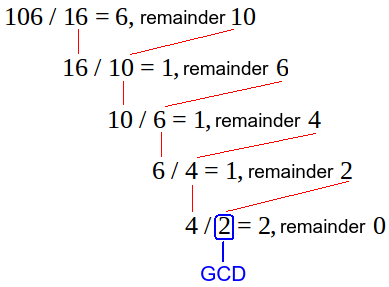
증명
증명은 다음과 같이 간단하게 할 수 있다.
gcd(a, b) = G, gcd(a, r) = G' 이라 하자. 여기서 적당한 서로소인 정수 A, B에 대해 가 성립한다.
이를 a = bq + r에 대입하면, GA = GBq + r 이고, r = G(A-Bq)이다. 여기서 G는 b와 r의 공약수임을 알 수 있다.
즉, G는 G'의 약수이므로 로 둘 수 있다.
그러면 적당한 서로소인 두 정수 k,l에 대해 GB = G'k = Gmk, G(A - Bq) = G'l = 이 성립한다. 이 식에서 각 변을 G로 나누면 B = mk, A - Bq = ml이다.
A = ml + Bq = ml + mkq = m(l + kq)에서 m은 와 B의 공약수인데, gcd(A, B) = 1이므로 항상 m = 1이고 G' = G이다.
이처럼 유클리드 호제법을 이용하면 최대공약수, 즉 GCD(Greatest Common Divisor)을 간단하게 구할 수 있다.
최대공약수 구현
단순 반복문을 사용하여 구현할 수도 있고, 재귀함수를 사용할 수도 있다. b > a 일때 따로 처리하지 않는것에 주목하자. b > a 일 경우 다음 호출은 자동으로 gcd(a, b)가 되기 때문이다.
반복문 사용
def gcd(a, b):
while b > 0:
a, b = b, a % b
return a재귀함수 사용
def gcd(a, b):
if a % b == 0: # 기저 조건
return b
return gcd(b, a % b)최소공배수 구현
최대공약수를 구하면 최소공배수 또한 간단하게 구할 수 있는데, 이는 최소공배수와 최대공약수 사이에 아래과 같은 성질이 성립하기 때문이다. 두 자연수 A, B를 최대공약수 G로 나누었을때, 최소공배수 L은 다음과 같이 나타낼 수 있다.

결국 GCD × LCM = A × B 이므로, 최소공배수 LCM을 구하려면 (A × B) // GCD를 해주면 된다는 것이다.
def lcm(a, b):
return a * b // gcd(a, b)'BOJ > 이론' 카테고리의 다른 글
| 중국인의 나머지 정리(Chinese Remainder Theorem, CRT) (0) | 2024.09.29 |
|---|---|
| Extended Euclidean Algorithm (확장된 유클리드 호제법) (0) | 2024.09.23 |
| 조합(Combination)과 이항 계수를 python으로 구현해보자. (0) | 2024.07.20 |
| python3 math 모듈 없이 올림, 내림, 반올림 하는법 (0) | 2024.07.13 |
