문제
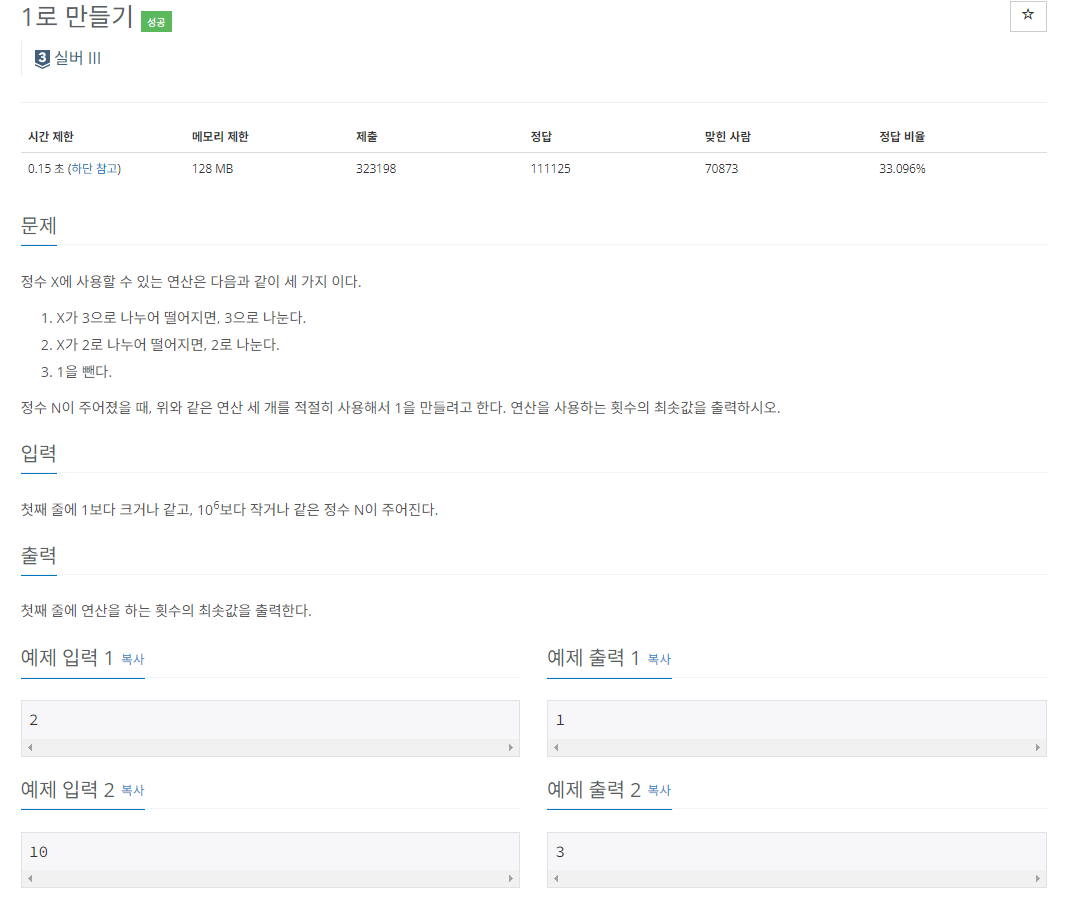
정수 X를 주어진 연산을 이용해 1을 만드는 방법들 중 최솟값을 구하는 방법이다.
시간 제한은 0.15초로 여유롭지 않은 것을 알 수 있다. python은 1.5초, pypy는 0.7초이다.
시간 초과 코드
import sys
def solve(a):
if a == int(a):
a = int(a)
if a == 1:
return 0
if L[a] != -1:
return L[a]
else:
t = min(1+solve(a/3), 1+solve(a/2), 1+solve(a-1))
L[a] = t
return t
else:
return 999
n = int(input())
L = [-1] * (n+1)
print(solve(n))처음 문제를 풀때는 재귀함수를 이용해 모든 경우의 수를 탐색하려고 했으나 시간 초과가 발생해서 dp를 이용해서 풀어보았다.
코드
def solve(n):
dp = [0] * (n + 1)
for i in range(2, n + 1):
dp[i] = dp[i-1] + 1
if i % 2 == 0:
dp[i] = min(dp[i], dp[i//2] + 1)
if i % 3 == 0:
dp[i] = min(dp[i], dp[i//3] + 1)
return dp[n]
n = int(input())
print(solve(n))dp 배열을 만들어서 해당 인덱스의 수가 1이 되는데 필요한 연산 횟수의 최솟값을 저장한다. 이후에는 dp 인덱스를 참고해서 중복되는 연산을 없앤다.
정답을 맞추고 더 효율적인 방법을 찾아보니 내가 푼 방식은 dp 방식중 바텀업 방식이고, 탑다운 방식으로 푼 사람도 있고, BFS로 풀이한 사람도 있었다. 정답 코드들의 시간과 메모리 사용량을 보니 BFS하고 탑다운 방식으로 푼 사람들이 더 효율적으로 푼것 같았다. 바텀업으로 구현할지 탑다운으로 구현할지 잘 고민해보고 풀어야겠다.
'BOJ > 문제' 카테고리의 다른 글
| [python3] 백준 23062번 - 백남이의 여행 준비의 준비 (0) | 2024.10.02 |
|---|---|
| [python3] 백준 3955번 - 캔디 분배 (0) | 2024.09.26 |
| [python3] 백준 11726번 - 2×n 타일링 (0) | 2024.09.11 |
| [python3] 백준 11050번 - 이항 계수 1 (0) | 2024.07.25 |
| [python3] 백준 2609번 - 최대공약수와 최소공배수 (0) | 2024.07.19 |
문제

정수 X를 주어진 연산을 이용해 1을 만드는 방법들 중 최솟값을 구하는 방법이다.
시간 제한은 0.15초로 여유롭지 않은 것을 알 수 있다. python은 1.5초, pypy는 0.7초이다.
시간 초과 코드
import sys
def solve(a):
if a == int(a):
a = int(a)
if a == 1:
return 0
if L[a] != -1:
return L[a]
else:
t = min(1+solve(a/3), 1+solve(a/2), 1+solve(a-1))
L[a] = t
return t
else:
return 999
n = int(input())
L = [-1] * (n+1)
print(solve(n))처음 문제를 풀때는 재귀함수를 이용해 모든 경우의 수를 탐색하려고 했으나 시간 초과가 발생해서 dp를 이용해서 풀어보았다.
코드
def solve(n):
dp = [0] * (n + 1)
for i in range(2, n + 1):
dp[i] = dp[i-1] + 1
if i % 2 == 0:
dp[i] = min(dp[i], dp[i//2] + 1)
if i % 3 == 0:
dp[i] = min(dp[i], dp[i//3] + 1)
return dp[n]
n = int(input())
print(solve(n))dp 배열을 만들어서 해당 인덱스의 수가 1이 되는데 필요한 연산 횟수의 최솟값을 저장한다. 이후에는 dp 인덱스를 참고해서 중복되는 연산을 없앤다.
정답을 맞추고 더 효율적인 방법을 찾아보니 내가 푼 방식은 dp 방식중 바텀업 방식이고, 탑다운 방식으로 푼 사람도 있고, BFS로 풀이한 사람도 있었다. 정답 코드들의 시간과 메모리 사용량을 보니 BFS하고 탑다운 방식으로 푼 사람들이 더 효율적으로 푼것 같았다. 바텀업으로 구현할지 탑다운으로 구현할지 잘 고민해보고 풀어야겠다.
'BOJ > 문제' 카테고리의 다른 글
| [python3] 백준 23062번 - 백남이의 여행 준비의 준비 (0) | 2024.10.02 |
|---|---|
| [python3] 백준 3955번 - 캔디 분배 (0) | 2024.09.26 |
| [python3] 백준 11726번 - 2×n 타일링 (0) | 2024.09.11 |
| [python3] 백준 11050번 - 이항 계수 1 (0) | 2024.07.25 |
| [python3] 백준 2609번 - 최대공약수와 최소공배수 (0) | 2024.07.19 |
