문제
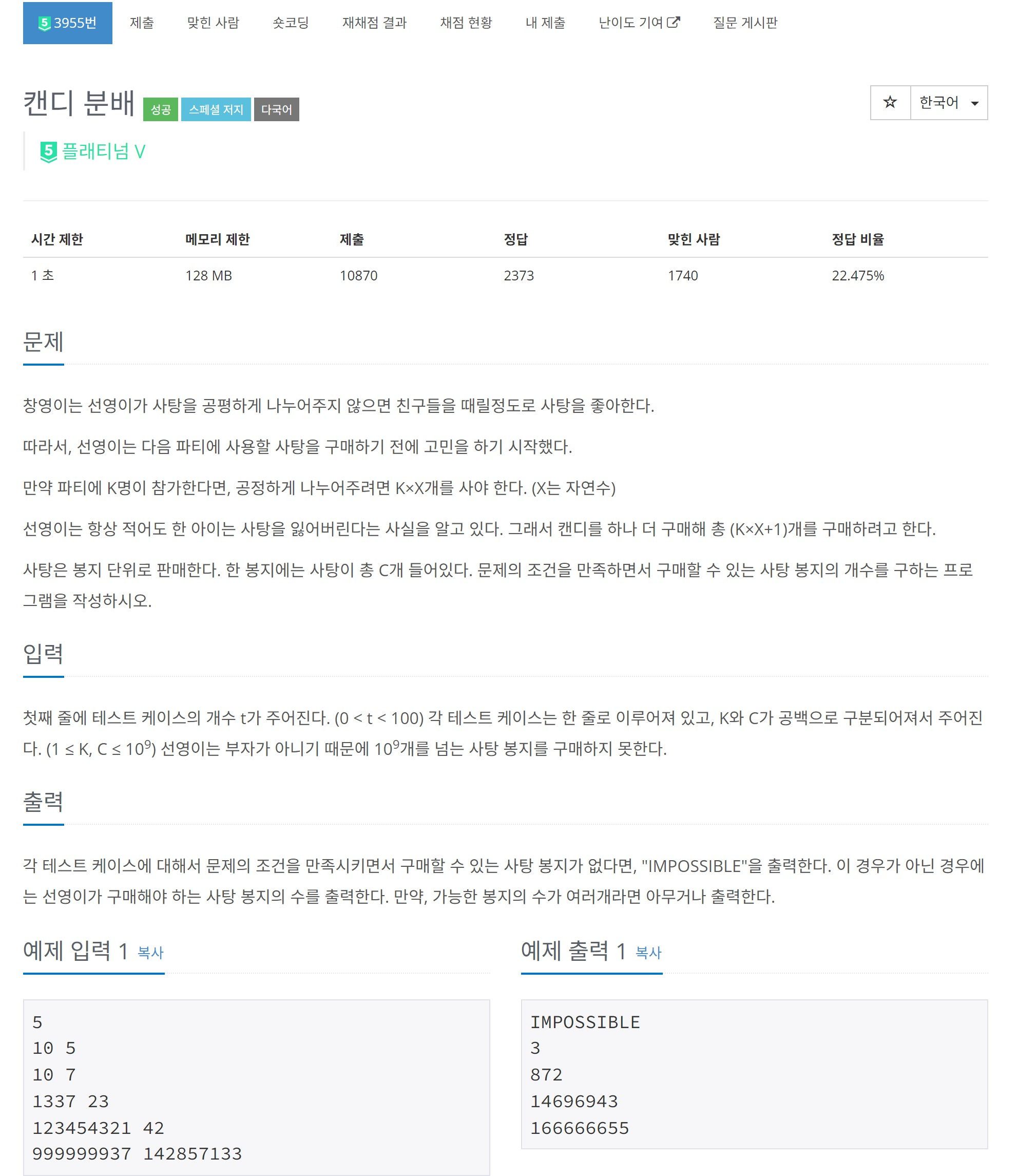
나의 첫 플레티넘 문제이다!! 이전 글에서 확장된 유클리드 알고리즘을 공부한것이 큰 도움이 되었다.
2024.09.23 - [BOJ/이론] - Extended Euclidean Algorithm (확장된 유클리드 호제법)
Extended Euclidean Algorithm (확장된 유클리드 호제법)
확장된 유클리드 호제법이란?2024.07.18 - [BOJ/이론] - 유클리드 호제법과 최대공약수, 최소공배수 python으로 구현하기 유클리드 호제법과 최대공약수, 최소공배수 python으로 구현하기유클리드 호
nivr4y.tistory.com
문제에서 요구하는 것을 식으로 만들어 보면 다음과 같다.
$$ k \cdot x + c \cdot y \equiv 1 \mod c $$
이는 확장된 유클리드 알고리즘으로 해를 구할 수 있다.
풀이
def eea(a, b):
x,y, u,v = 0,1, 1,0
while b != 0:
q, r = a//b, a%b
m, n = x-u*q, y-v*q
a,b, x,y, u,v = b,r, u,v, m,n
gcd = a
return gcd, x, y
for _ in range(int(input())):
k,c= map(int,input().split())
g,x,y = eea(k,c)
if x<=0 or y==0:
y -= c
x = (k*y-1)//c
print('IMPOSSIBLE' if g!=1 or abs(x) > 10**9 else abs(x))베주 항등식의 해는 유일하지 않고, 여러개가 있기 때문에 x<=0이거나 y==0일때(사람이 0보다 적거나 사야할 사탕 봉지의 수가 0일때) 베주 항등식의 일반적인 해의 형태에 맞게 바꾸어주었다.
$$ x = x_0 + \frac{b}{g}n, \quad y = y_0 - \frac{a}{g}n $$
x가 $10^9$이상 될 수 없다는 조건 때문에 조금 해맸다.
정수론 이론을 조금만 공부하니 기초적인 문제이지만 플레티넘 문제도 도전할 수 있게 되었다. 공부할 의욕이 솟아난다.
'BOJ > 문제' 카테고리의 다른 글
| [python3] 백준 31478번 - 포니 양은 놀고 싶어! (0) | 2024.10.04 |
|---|---|
| [python3] 백준 23062번 - 백남이의 여행 준비의 준비 (1) | 2024.10.02 |
| [python3] 백준 11726번 - 2×n 타일링 (0) | 2024.09.11 |
| [python3] 백준 1463번 - 1로 만들기 (0) | 2024.08.21 |
| [python3] 백준 11050번 - 이항 계수 1 (0) | 2024.07.25 |
문제

나의 첫 플레티넘 문제이다!! 이전 글에서 확장된 유클리드 알고리즘을 공부한것이 큰 도움이 되었다.
2024.09.23 - [BOJ/이론] - Extended Euclidean Algorithm (확장된 유클리드 호제법)
Extended Euclidean Algorithm (확장된 유클리드 호제법)
확장된 유클리드 호제법이란?2024.07.18 - [BOJ/이론] - 유클리드 호제법과 최대공약수, 최소공배수 python으로 구현하기 유클리드 호제법과 최대공약수, 최소공배수 python으로 구현하기유클리드 호
nivr4y.tistory.com
문제에서 요구하는 것을 식으로 만들어 보면 다음과 같다.
이는 확장된 유클리드 알고리즘으로 해를 구할 수 있다.
풀이
def eea(a, b):
x,y, u,v = 0,1, 1,0
while b != 0:
q, r = a//b, a%b
m, n = x-u*q, y-v*q
a,b, x,y, u,v = b,r, u,v, m,n
gcd = a
return gcd, x, y
for _ in range(int(input())):
k,c= map(int,input().split())
g,x,y = eea(k,c)
if x<=0 or y==0:
y -= c
x = (k*y-1)//c
print('IMPOSSIBLE' if g!=1 or abs(x) > 10**9 else abs(x))베주 항등식의 해는 유일하지 않고, 여러개가 있기 때문에 x<=0이거나 y==0일때(사람이 0보다 적거나 사야할 사탕 봉지의 수가 0일때) 베주 항등식의 일반적인 해의 형태에 맞게 바꾸어주었다.
x가 이상 될 수 없다는 조건 때문에 조금 해맸다.
정수론 이론을 조금만 공부하니 기초적인 문제이지만 플레티넘 문제도 도전할 수 있게 되었다. 공부할 의욕이 솟아난다.
'BOJ > 문제' 카테고리의 다른 글
| [python3] 백준 31478번 - 포니 양은 놀고 싶어! (0) | 2024.10.04 |
|---|---|
| [python3] 백준 23062번 - 백남이의 여행 준비의 준비 (1) | 2024.10.02 |
| [python3] 백준 11726번 - 2×n 타일링 (0) | 2024.09.11 |
| [python3] 백준 1463번 - 1로 만들기 (0) | 2024.08.21 |
| [python3] 백준 11050번 - 이항 계수 1 (0) | 2024.07.25 |
