문제
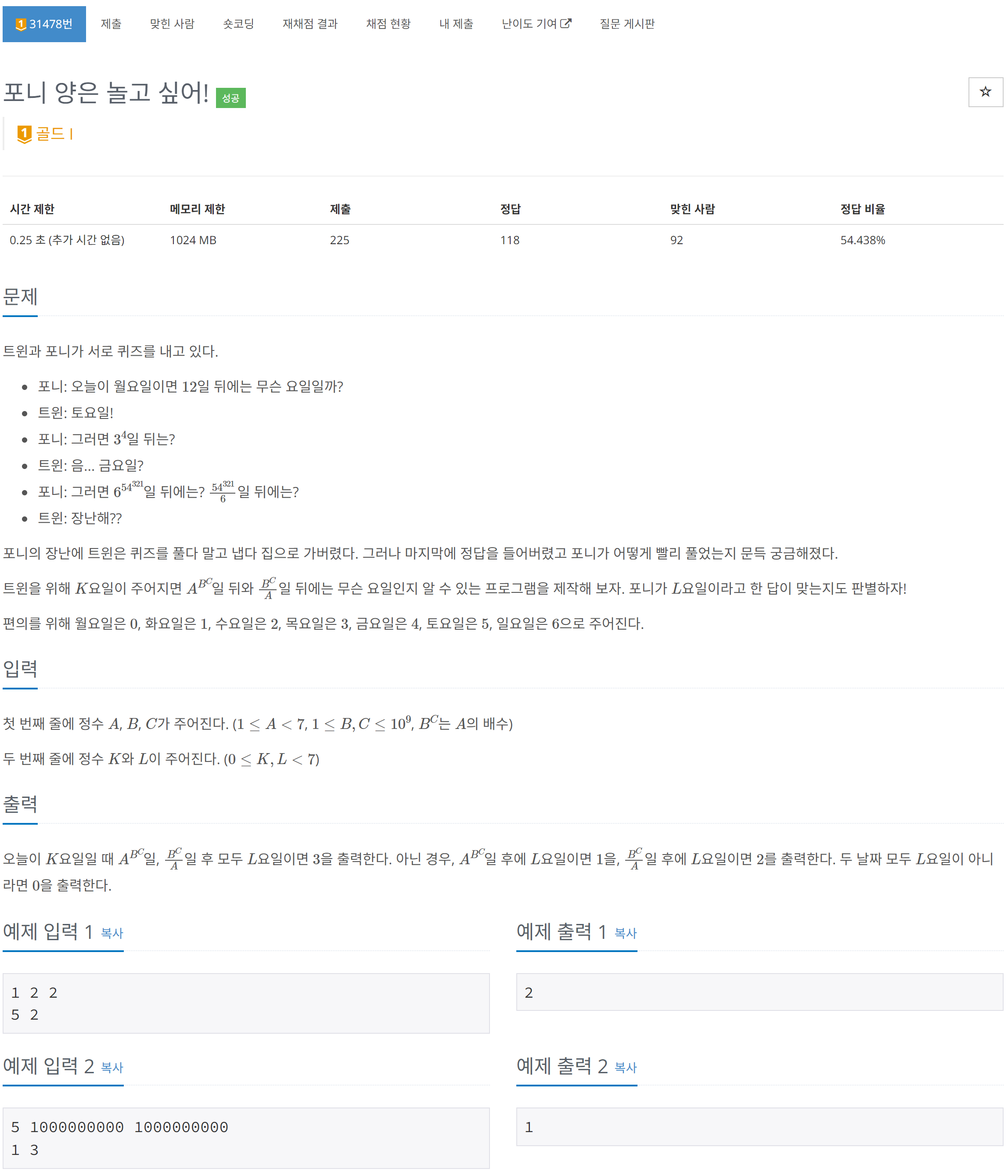
간단한 정수론 문제이다.
$$ A^{B^C}, B^C / A$$
결국 이 두개를 0.25초 안에 계산하면 되는 문제라고 볼 수 있다.
첫번째의 경우에는 페르마의 소정리를 이용하면 간단하게 구할 수 있다. 페르마의 소정리는 아래과 같다.
$$ p\text{가 소수이면, 모든 정수 }a\text{에 대해 } a^p\equiv a\left({\rm mod}\ p\right) \text{이다.}$$
이는 동치인 아래의 정리로 바꿀 수 있다.
$$ p\text{가 소수이면, 모든 정수 }a\text{에 대해 } a^{p-1}\equiv 1\left({\rm mod}\ p\right) \text{이다.}$$
우리는 아래의 정리를 사용할 것이다. $ A^{7-1}\equiv 1\left({\rm mod}\ 7\right) $ 이기 때문에, 우리는 A의 지수인 $B^C$에 mod 6을 취할 수 있다.
두번째의 경우에는 A와 7이 서로소 관계이기 때문에, pow(A,-1,7)을 통해 곱셈역원을 곱해줘도 되고, 나는 그냥 B하나를 떼서 A로 나누어준 후 pow 계산을 했다.
풀이
a,b,c = map(int,input().split())
k,l = map(int,input().split())
n = (k + pow(a,pow(b,c,6),7)) % 7
m = (k + (b//a)*pow(b,c-1,7)) % 7
if n==l and m==l:
print(3)
elif n==l:
print(1)
elif m==l:
print(2)
else:
print(0)
'BOJ > 문제' 카테고리의 다른 글
| [python3] 백준 5525번 - IOIOI (1) | 2024.10.05 |
|---|---|
| [python3] 백준 23062번 - 백남이의 여행 준비의 준비 (1) | 2024.10.02 |
| [python3] 백준 3955번 - 캔디 분배 (0) | 2024.09.26 |
| [python3] 백준 11726번 - 2×n 타일링 (0) | 2024.09.11 |
| [python3] 백준 1463번 - 1로 만들기 (0) | 2024.08.21 |
문제

간단한 정수론 문제이다.
결국 이 두개를 0.25초 안에 계산하면 되는 문제라고 볼 수 있다.
첫번째의 경우에는 페르마의 소정리를 이용하면 간단하게 구할 수 있다. 페르마의 소정리는 아래과 같다.
이는 동치인 아래의 정리로 바꿀 수 있다.
우리는 아래의 정리를 사용할 것이다. 이기 때문에, 우리는 A의 지수인 에 mod 6을 취할 수 있다.
두번째의 경우에는 A와 7이 서로소 관계이기 때문에, pow(A,-1,7)을 통해 곱셈역원을 곱해줘도 되고, 나는 그냥 B하나를 떼서 A로 나누어준 후 pow 계산을 했다.
풀이
a,b,c = map(int,input().split())
k,l = map(int,input().split())
n = (k + pow(a,pow(b,c,6),7)) % 7
m = (k + (b//a)*pow(b,c-1,7)) % 7
if n==l and m==l:
print(3)
elif n==l:
print(1)
elif m==l:
print(2)
else:
print(0)
'BOJ > 문제' 카테고리의 다른 글
| [python3] 백준 5525번 - IOIOI (1) | 2024.10.05 |
|---|---|
| [python3] 백준 23062번 - 백남이의 여행 준비의 준비 (1) | 2024.10.02 |
| [python3] 백준 3955번 - 캔디 분배 (0) | 2024.09.26 |
| [python3] 백준 11726번 - 2×n 타일링 (0) | 2024.09.11 |
| [python3] 백준 1463번 - 1로 만들기 (0) | 2024.08.21 |
